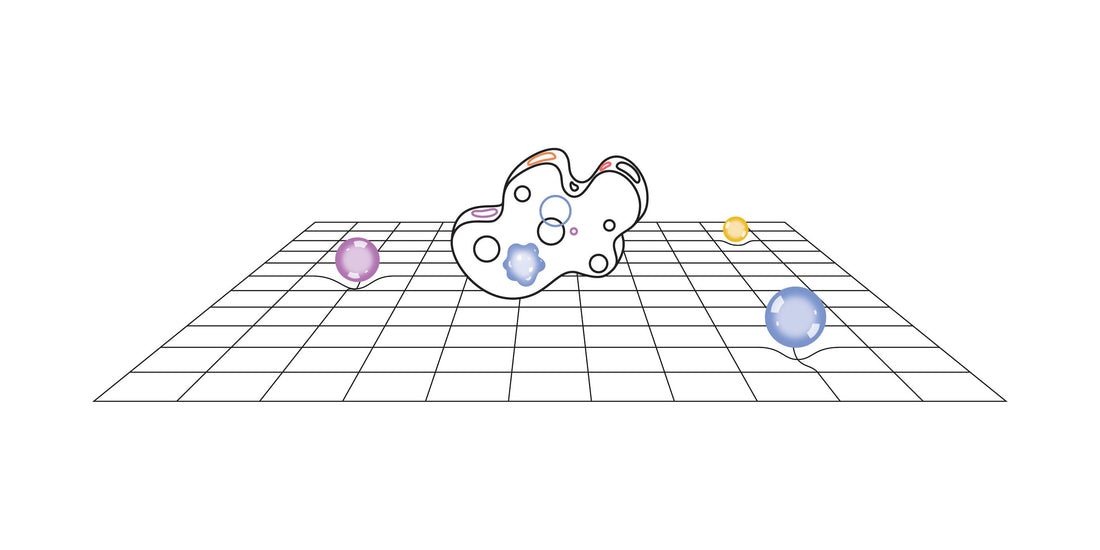
Your idea space consists of your thoughts, emotions, sensations, perceptions and the empty set, ∅. Your idea space is unique to you, uncountable, and has zero measure.

Figure 1. Your idea space consists of your thoughts, emotions, sensations, perceptions, and the empty set, ∅.
Overall, an idea space is a mathematical representation of your mind and is the trivial solution to Einstein's field equation: \[R_{\mu \nu} - {1 \over 2}g_{\mu \nu}\,R + g_{\mu \nu} \Lambda = {8 \pi G \over c^4} T_{\mu \nu} ,\] where \(g_{\mu \nu}\) is the metric, \(R_{\mu \nu}\) is the Ricci Tensor, \(R\) is the Ricci Scalar, \(G\) is Newton's gravitational constant (\(6.7 \times 10^{-11} {m^3 \over {kg \cdot s^2}}\)), \(c\) is the speed of light (\(186,000\) miles per second), \(\Lambda\) is the cosmological constant, and \(T_{\mu \nu}\) is the energy-momentum tensor.
In short, the equation tells you how spacetime (left hand portion) curves in relation to matter (right hand portion) to create the illusion of gravity. As Steven Weinberg says, “In my view, it is much more useful to regard general relativity above all as a theory of gravitation.”
A classic example is that of a trampoline. Imagine placing a bowling ball in the middle of a trampoline. When you do, the trampoline dips. If you were to roll some marbles around the bowling ball, then the marbles would “gravitate” towards the bowling ball. In this instance, the trampoline represents spacetime and the bowling ball represents matter and radiation (e.g. stars, planets, light, etc.). Gravity is simply an illusion caused by the curvature of spacetime.

Figure 2. Matter curves spacetime to create the illusion of gravity.
Einstein’s field equation is rooted around the metric, \(g_{\mu \nu}\). The metric defines the distance between two points in spacetime. For instance, you may be familiar with the Euclidean metric, which looks like the Pythagorean Theorem: \[distance^2=a^2+b^2+c^2.\]An idea space follows the pseudometric, which means the metric is zero: \[g_{\mu \nu}=0.\]
Simply put, the distance between any idea (thought, emotion, sensation, or perception), relative to an outside observer, is zero. In other words, your idea space has zero measure and looks like nothing, ∅, to the outside world. However, simply because it looks like there is nothing there does not mean there is nothing there. Behind the veil of nothingness can lie an uncountable depth, like your idea space.

Figure 3. The metric, \(g_{\mu \nu}\), of an idea space is zero, \(0\), which looks like nothing,∅. However, \(0\neq\)∅. Behind an object of zero measure can lie uncountable depth, like your idea space.
The Ricci Tensor, \(R_{\mu \nu}\), and Ricci Scalar, \(R\), are based on the metric and can be obtained via the following relations. Once you have the metric, \(g_{\mu \nu}\), you take its derivative to obtain the Christoffel Symbols, \(\Gamma^{\sigma}_{\mu\nu}\). From there, you take the derivative of the Christoffel Symbols to obtain the Riemann Tensor, \(R^{\rho}{}_{\sigma\mu\nu}\). The Riemann Tensor contracts to the Ricci Tensor, \(R_{\mu \nu}\). And, finally, taking the trace of the Ricci Tensor produces the Ricci Scalar, \(R\). These relations are stated more explicitly through the below equations:
\[\Gamma^{\sigma}_{\mu\nu}={1 \over 2} g^{\sigma\rho}(\partial_{\mu}g_{\nu\rho} + \partial_{\nu}g_{\rho\mu} + \partial_{\rho}g_{\mu\nu});\]
\[R^{\rho}{}_{\sigma\mu\nu}=\partial_{\mu}\Gamma^{\rho}_{\nu\sigma}-\partial_{\nu}\Gamma^{\rho}_{\mu\sigma}+\Gamma^{\rho}_{\mu\lambda}\Gamma^{\lambda}_{\nu\sigma}-\Gamma^{\rho}_{\nu\lambda}\Gamma^{\lambda}_{\mu\sigma};\]
\[R_{\mu\nu}=R^{\lambda}{}_{\mu\lambda\nu};\]
\[R=R^{\mu}{}_{\mu}=g^{\mu\nu}R_{\mu\nu}.\]
Since the metric, \(g_{\mu \nu}\), of your idea space is zero, then the Christoffel Symbols, or the derivative of the metric, are also zero:
\[\Gamma^{\sigma}_{\mu\nu}=0.\]
This is because the derivative of zero, is zero. The derivate of the Christoffel Symbols is represented by the Riemann tensor, \(R^{\rho}{}_{\sigma\mu\nu}\), which also becomes zero by the same logic:
\[R^{\rho}{}_{\sigma\mu\nu}=0.\]
Therefore, the Ricci Tensor, \(R_{\mu \nu}\), and Ricci Scalar, \(R\), are both zero since the contraction and trace of zero are both zero. Explicitly,
\[R_{\mu\nu}=R=0.\]
Going back to Einstein’s field equation and inserting the values for the metric, \(g_{\mu \nu}\), the Ricci Tensor, \(R_{\mu \nu}\), and Ricci Scalar, \(R\), produces the trivial solution:
\[0={8\pi G \over c^4}T_{\mu\nu}.\]
Here, we see the energy-momentum tensor, \(T_{\mu \nu}\), of an idea space is 0. In other words, your idea space (all your thoughts, emotions, sensations, and perceptions) has zero direct effect on spacetime. In terms of the trampoline, an idea space would cause the trampoline to not dip at all.

Figure 4. An idea space has no direct effect on spacetime, while matter or energy directly affects spacetime.
To test that your idea space has zero measure, do the following experiment. Hold something in your hand, like your phone or computer. Clearly, you can measure it. You can feel it. Others can see it. Now, close your eyes and create a mental image of what you’re holding. Can anyone else see the image you produced in your head? No—it has zero measure and therefore looks like nothing to an outside observer. Is there nothing there? No—clearly there is something there. Something only you can see. This holds true for all your thoughts, emotions, sensations, and perceptions. No one else can see them, but you.
All in all, an idea space is a mathematical model used to describe the mind in a way that is congruent with modern physics. It is the trivial solution to Einstein's field equation.
For more information, check out the whitepaper, idea space cards, and sign up for the newsletter on the home page!