What's The Big Picture?
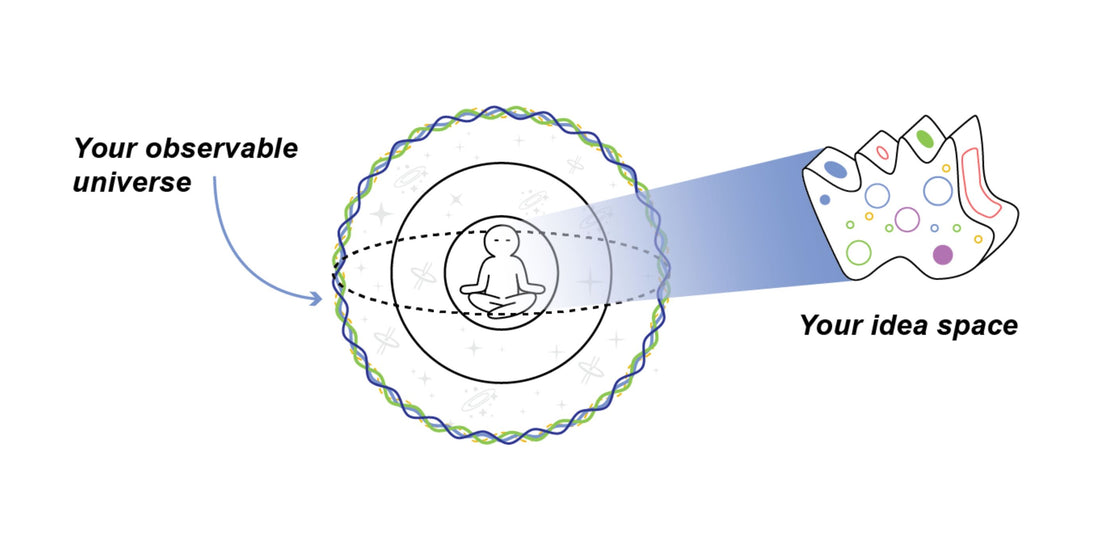
Everyone lives at the center of their own observable universe.
Your observable universe is a giant sphere centered on you where everything you see is in the past. Why? Because it takes time for light to travel from point A to point B, even when traveling at \(186,000\) miles per second. Your observable universe is filled with celestial objects, like galaxies, stars, planets, and humans. Since everything you see is in the past, the edge of your observable universe is its beginning: The Big Bang.
What lies at the center of this beautiful system? Your idea space.

Figure 1. Your idea space lies at the center of your observable universe.
What's Your Idea Space?
As we saw in the last blog, an idea space is the trivial solution to Einstein's field equation. In other words, your idea space (all your thoughts, emotions, sensations, and perceptions) has zero measure and looks like nothing to everyone else.

Figure 2. Your idea space consists of your thoughts, emotions, sensations, and perceptions. Your idea space looks like nothing to the outside world.
To test this, simply hold something in your hand, like your phone or computer. Clearly, others can see and measure it. Now, close your eyes and create a mental image of what you're holding. Can anyone else see the mental image in your mind? No... Now, is there nothing there? No... Clearly, there is something there. Something only you can see: your idea space.
That said, while an idea space is the trivial solution to Einstein's field equation, an idea space is not the only exact solution. In fact, there are a couple other metrics that are exact solutions to Einstein's field equation. This post explores these metrics in more detail. But first, what even is a metric?
What's a Metric?
A metric, \(d\), is simply how you define the distance between two points. The regular, or Euclidean, distance between any two points is simply \(x-y\), or \(d(x,y)\). The metric can be written in many ways, and physicists like to write the metric as \(g_{\mu\nu}.\) To see how the metric relates to Einstein's field equation, check out the last blog.
Independent of nomenclature, a metric has three main properties:
Positive Definiteness
The distance between any two points is positive. The distance between two points is zero if and only if the two points are the same point, or at the same location:

\[d(x,y)\geq0,\]
\[d(x,y)=0 \textrm{ if and only if }x=y.\]
Figure 3. Positive Definiteness.
Symmetry
The distance between \(x\) and \(y\) is the same as the distance between \(y\) and \(x\):

\[d(x,y)=d(y,x).\]
Figure 4. Symmetry.
Triangle Inequality
The distance between \(x\) and \(y\), plus the distance between \(y\) and \(z\), must be greater than or equal to the distance between \(x\) and \(z\):

\[d(x,y)+d(y,z)\geq d(x,z) \textrm{ for all } x, y, z.\]
Figure 5. Triangle Inequality.
Pseudometric
A pseudometric is one where the first condition allows for the distance between any two, unique points to be zero for any \(x\) and \(y\):

\[d(x,y)=0 \textrm{ for any } x \textrm{ and } y.\]
Figure 6. Pseudometric.
What are Metrics in General Relativity?
General relativity dictates how spacetime curves in relation to matter, or energy. Specifically, according to general relativity, the universe is made up of different types of metrics. Each metric proves useful in figuring out distances in their respective domains.
For instance, in day to day life, we may use the Euclidean Metric to measure the distance between any two points. If you are a physicist, then you may use the Minkowski Metric. Near stationary stars, we may switch to the Schwarzschild Metric. For charged stars, we use the Reissner-Nordström Metric. For spinning stars, we turn to the Kerr Metric. To look at the observable universe as a whole, we use the Robertson-Walker Metric. To describe consciousness, we use an idea space.
Euclidean Metric
The Euclidean Metric is your typical way to measure spatial distances. Think Pythagorean Theorem in three dimensions:

\[d(x,y,z)^2 = x^2+y^2+z^2.\]
Figure 7. Euclidean distance.
Minkowski Metric
The Minkowski Metric describes a flat spacetime, or special relativity. This is important, because according to the Einstein Equivalence Principle in small enough regions of spacetime, the laws of physics reduce to those of special relativity. The Minkowski Metric looks like the Pythagorean Theorem in four dimensions:

where \(x, y, z\) represent spatial coordinates, \(t\) is time, and \(c\) is the speed of light (\(186,000\) miles per second).
Schwarzschild Metric
The Schwarzschild Metric represents the space around a spherically non-spinning, symmetrical object. It's metric is a little more complicated and looks like this:

where \(x, y, z\) are turned into the spherical coordinates \(r, \theta, \phi\) whose origin is at the center of the sphere, \(G\) is Newton's gravitational constant (\(6.7 \times 10^{-11} {m^3 \over {kg \cdot s^2}}\)), and \(M\) is the mass of the object.
Robertson-Walker Metric
The Robertson-Walker Metric describes an expanding, homogenous, and isotropic universe, also in spherical coordinates. In other words, it describes your observable universe: a giant sphere centered on you. The metric looks like this:

\[d(t, r,\theta, \phi)^2=(c \cdot dt)^2 - a^2(t)[ {dr^2 \over 1-kr^2 }+r^2(d\theta^2+sin^2\theta \textrm{ }d\phi^2)]\] \[d(t, r,\theta, \phi)^2=(c \cdot dt)^2 - a^2(t)[ {dr^2 \over 1-kr^2 }+\] \[r^2(d\theta^2+sin^2\theta \textrm{ }d\phi^2)]\]
Figure 10. The Robertson-Walker Metric describes the observable universe: a giant sphere centered on you.
where \(a\) describes the rate of acceleration as a function of time, \(t\), and \(k\) is a curvature parameter describing an open, closed, or flat universe (our universe is believed to be "flat" on large scales).
Idea Space Metric
The Idea Space describes the mind and is represented by the pseudometric. In other words, the distance between any two points (thoughts, emotions, sensation, or perception) is zero to an outside observer. This is represented as:

Figure 11. Your idea space has zero measure.
For more information, check out the whitepaper, idea space cards, and sign up for the newsletter on the home page!